OpenOffice.cz - web věnovaný kancelářským balíkům OpenOffice.org

Maďarská společnost MultiRacio Ltd. se nedávno blýskla opravdovým klenotem. Na svém webu ale také v repozitáři OpenOffice.org objevíte velmi zajímavý plugin pro vykreslování pohybů nebeských těles kolem Slunce – Planet´s Orbit .

Plugin si můžete stáhnout na stránce EuroOffice Planets webu MultiRacio Ltd. a na stránce s rozšířeními OpenOffice.org.

Trocha teorie na úvod…

Tělesa se kolem Slunce nepohybují po kružnicích, ale po elipsách. Tento poznatek objevil německý matematik Johannes Kepler během svého pobytu v Praze (v letech 1600 až 1612). Kepler v Praze na základě pozorování pohybů planet od Tychona Braheho sestrojil dva ze svých pohybových zákonů a spolu se třetím, objeveným již dříve, mají dnes tuto podobu:

1. Planety se pohybují kolem Slunce po elipsách a Slunce je v ohnisku těchto elips.
2. Plochy opsané průvodičem planety jsou za stejnou dobu stejné.
3. Dvojmoci oběžných dob planet jsou v tomtéž poměru jako trojmoci velkých poloos jejich drah:

   

   Jednotkou času je rok, jednotkou vzdálenosti astronomická jednotka (AU – astronomical unit), což je střední vzdálenost Země od Slunce – 149,597 · 10⁹ m.

Elipsa je – podobně jako kružnice – kuželosečka, tedy křivka, kterou lze získat řezem kužele pod určitým úhlem vůči základně. Je-li úhel nulový, vznikne kružnice. Pokud je úhel v intervalu (0,90) stupňů, máme elipsu. Při úhlu řezu rovnému 90 ° vznikne parabola a při úhlech větších vznikne hyperbola.

Aby se v nebeské mechanice zdůraznily rozdíly v pohybu tělesa kolem Slunce oproti pohybu po kružnici, mluví astronomové o tzv. anomálii . Anomálií rozumíme úhel tělesa pohybujícího se po elipse, v určitém časovém okamžiku. Tehdy se těleso nachází v bodě T (viz obrázek).

 

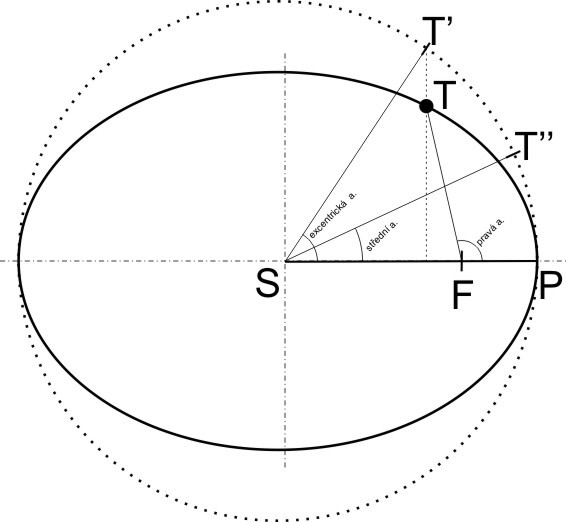Co je to v nebeské mechanice anomálie…

 

V astronomii je trojí pojetí anomálií v souvislosti s pohybem po elipse, které je třeba rozebrat:

• pravá anomálie : je to úhel mezi přímkou spojující ohnisko elipsy a perihélium a přímkou spojující ohnisko s polohou tělesa; značí se v ;

• excentrická anomálie : jestliže sestrojíme kolem středu elipsy kružnici se stejným poloměrem, jaký má její velká poloosa, a spustíme z této kružnice kolmici na poloosu tak, aby protínala bod T , protne tato kolmá přímka kružnici v bodě T' ; úhlu mezi středem elipsy, perihelem a bodem T' (s vrcholem ve středu elipsy) se říká excentrická anomálie a značí se E ;

• střední anomálie : je to úhel mezi periheliem, středem elipsy a bodem T'' na kružnici; tento bod odpovídá pohybu tělesa po imaginární kružnici za stejnou dobu oběhu. To znamená, že výpočtem střední anomálie zjistíme polohu tělesa na elipse v určité době; tím získáme i hodnotu pravé anomálie. Střední anomálie se řeší prostřednictvím Keplerovy rovnice :

  M = E – e sin E ,

  kde

  M … střední anomálie,

  e… číselná výstřednost

  

  kde a , b jsou velká, resp. malá poloosa elipsy.

Planet´s Orbit

Při spuštění se ukáže okno jako na následujícím obrázku. Z něj vybíráte důležité parametry pro projekci dráhy tělesa.

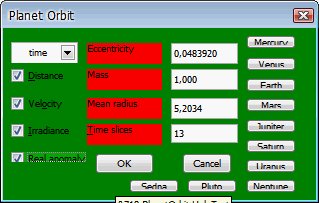Okno pro nastavení parametrů dráhy oběžnice

Parametry, které můžete volit, jsou tyto:

• time/relative time … první možnost měří uplynulý čas ve dnech, zatímco druhá škáluje čas podle orbitálního času, čas je tedy relativní vzhledem k oběžné době;
• eccentricity … volíte numerickou excentricitu (výstřednost) dráhy;
• mass … určujete hmotnost centrálního tělesa (Slunce), hmotnost oběžnice (například planety) se považuje za nulovou, jde o hmotný bod;
• mean radius … střední vzdálenost od Slunce;
• time slices … vepsáním čísla určujete počet časových kroků.

V pravé části okna můžete využít existujících těles ve sluneční soustavě (po klepnutí na příslušné tlačítko se parametry zadají automaticky – v tomto případě Jupiter). V levé části zaškrtnutím jednotlivých polí určíte, které parametry se zobrazí formou grafů a tabulek. Jde o tyto:

• distance … vzdálenost,
• velocity … rychlost,
• irradiance … stupeň ozáření oběžnice Sluncem,
• real anomaly … pravá anomálie.

Po zvolení hodnot a nastavení zobrazovaných hodnot stiskněte tlačítko OK . Po chvíli práce makra se do sešitu Calcu vloží výsledek – například takovýto:

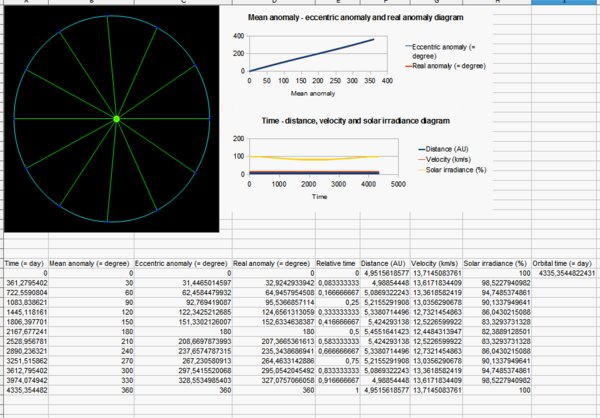Jak kolem Slunce obíhá Jupiter – výsledky nikoho nepřekvapí…

Jde o parametry dráhy Jupitera, takže žádné velké překvapení se nekoná. Na obrázku znázorňujícím tvar trajektorie kolem Slunce vidíte, že Jupiterova dráha je takřka kruhová – Jupiter se kolem Slunce pohybuje po téměř dokonalé kružnici, což lze vidět i v tabulkách a grafech. Na prvním grafu vidíte, že křivka putuje velmi rovnoměrně – diagonálně – z levého dolního rohu k pravému hornímu a můžete si povšimnout (pokud odečtete nějaké hodnoty), že tato křivka je v podstatě skutečně diagonálou. Jde o graf zachycující pravou anomálii, zde však vidíte, že prakticky neexistuje v tom smyslu, že se Jupiterova dráha neodlišuje od kružnice. Kdyby byla například hodně excentrická (to si ukážeme na dalším příkladu), měla by křivka jiný průběh. Zkuste již nyní uhodnout jaký.

Na druhém grafu vidíme tři křivky. Křivka znázorňující vzdálenost je konstantní – takže i zde vidíte, že se vzdálenost Jupitera od Slunce prakticky nemění. Tomu odpovídá i konstantní oběžná rychlost (dle Keplerových zákonů ) i téměř konstantní stupeň ozáření.

Diagramy nespadly z nebes, jsou závislé na datech v připojené tabulce, takže je můžete standardně upravovat a hodnoty v tabulce rovněž. Jak vidíte, tabulka obsahuje velké množství zajímavých hodnot. Kromě střední, excentrické a pravé anomálie (co tyto hodnoty znamenají, to si prostě musíte představit na základě výše uvedených informací, nejsou zcela intuitivní jako rychlost nebo vzdálenost) tu najdete informaci o vzdálenosti, rychlosti pohybu a stupni ozáření. Dále jsou tu hodnoty relativního času , který jsme si vysvětlili výše, a také dobu oběhu ve dnech. Celý oběh je rozdělen na třináct časových úseků (stejně velkých).

Podívejte se na příklad trochu zajímavější. Takovým může být případ oběžnice, která obíhá po dráze s velkou excentricitou. Můžete si zvolit jakékoliv fyzikálně a matematicky platné možnosti, ale využijte nabídky nechat si zobrazit průběh dráhy planetky Sedna coby prototypu dráhy s velkou excentricitou.

Nastavování parametrů oběhu planetky Sedna

Již ze zadání můžete (máte-li určité zkušenosti) očekávat velkou změnu. Nejdůležitější parametr je samozřejmě výstřednost, a ta je v tomto případě velmi výrazná. Připomínám, že výstřednost elipsy se pohybuje v intervalu (0,1). Křivka s výstředností rovnou jedné je parabola.

Výsledek je opravdu velmi zajímavý – viz přiložený obrázek.

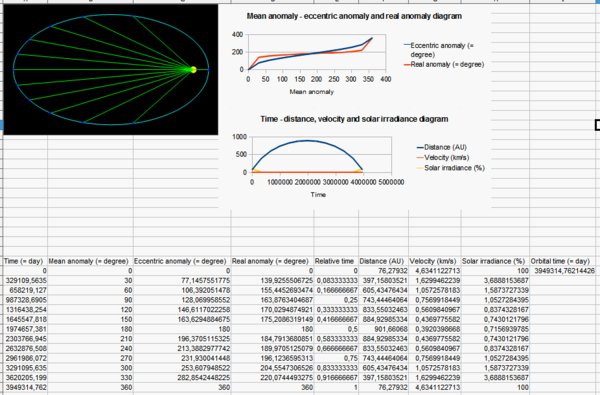Výsledná tabulka s grafy pro planetku Sedna

Kružnice se proměnila ve velmi protáhlou elipsu s velkou výstředností. Pronikavě se změnily diagramy a údaje v tabulce.

• Na obrázku čáry rozdělují časové úseky. Můžete tak vytušit i rychlost, s jakou se planetka pohybuje – v korespondenci s Keplerovými zákony.
• Na prvním diagramu můžete vidět, že Sedna se pohybuje v blízkosti Slunce rychleji, než kdyby se pohybovala po kružnici, a dále od Slunce zase pomaleji.
• To vystihuje i další graf, v němž můžete s pomocí křivky Distance a Velocity mapovat průběh rychlosti na vzdálenosti. Lépe je to ale vidět v tabulce a také tehdy, pokud si otevřete nový list a spustíte makro ještě jednou, ale v úvodním okně povolíte zobrazit jen graf rychlosti (aby se nepřekrýval s grafem vzdálenosti, který je jinak oškálovaný).

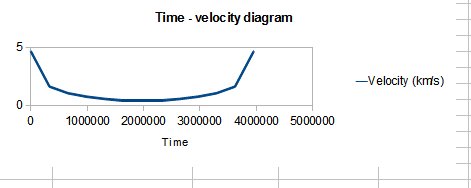Graf závislosti rychlosti oběžnice na čase

• V tabulce zjistíte, že Sedna se pohybuje kolem Slunce ve vzdálenosti v rozmezí 76 AU až neuvěřitelných 900 AU!! Všimněte si také, že v perihelu se pohybuje rychlostí, která je řádově stejná jako první kosmická rychlost.

Planets – animation

Součástí doplňku je i vykreslovací Java applet Planets – animation. Vykresluje pohyb oběžnice kolem Slunce při zadané hmotnosti centrálního tělesa (nemusí to být jen Slunce, samozřejmě), výstřednosti dráhy a střední vzdálenosti. Spolu s pohybem oběžnice zobrazuje i graf závislostí mezi střední, pravou a excentrickou anomálií. Tak lze například určit, ve kterých úsecích se oběžný pohyb zrychluje a o kolik a naopak.

Vykreslení pohybů planet kolem Slunce při zadaných parametrech

Applet se spouští následovně. V otevřeném sešitě vybereme z nabídky Nástroje položku Planets – Animation. Tím otevřeme dokument Writeru obsahující odkaz na daný applet. Ten je na OpenOffice.org nezávislý a lze jej tedy provozovat samostatně. Po klepnutí na odkaz (se stisknutou klávesou [Ctrl]) se applet otevře. Jde o dvě okna, v prvním jsou parametry a vykreslení pohybu, ve druhém se zobrazuje M-E a M-v diagram. Pro začátečníky je asi nejzajímavější první okno, pokročilejší ale ve druhém najdou velmi zajímavé informace.

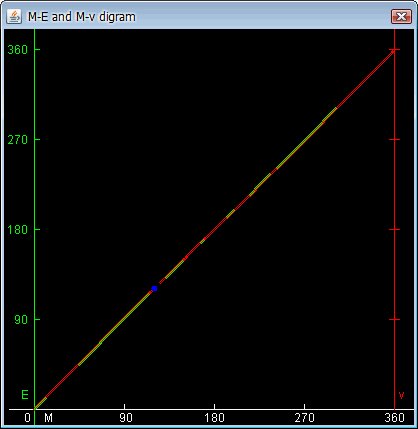V ME a Mv diagramu lze sledovat rozdíly reálného pohybu oběžnice v s pohybem kruhovým

Záhlaví prvního okna je: Demostration of Kepler´s second law. Připomínám, že tento zákon říká, že plošná rychlost (plocha opsaná průvodičem za určitý čas) planety je konstantní. Za stejnou dobu opíše průvodič planety stejnou plochu.

Jaké parametry lze zadat do prvního okna?

• Eccentricity … výstřednost vykreslované elipsy.
• Mass (solar mass) … hmotnost centrálního tělesa v jednotách Slunce, a to v intervalu (0, 1,8).
• Mean radius … střední vzdálenost oběžnice od centrálního tělesa.
• Line, Area … zaškrtnutím těchto polí určujete, zda chcete vykreslovat samotný průvodič (Line), a/nebo plochu opsanou průvodičem (Area).

Pozor, desetinná čísla je třeba dávat s tečkou, nikoliv čárkou.

Tlačítka mají následující význam:

• Start, Stop … spouštíte, resp. pozastavujete animaci.
• Reset … vrací oběžnici do výchozí polohy.
• Exit … ukončuje applet.

V informační části pod tlačítky se dozvíte hodnoty také již známých parametrů (v závorkách jsou jednotky): aktuální vzdálenost (Distance – AU), aktuální rychlost (Velocity – AU/den), relativní procento ozáření Sluncem (Solar irradiance – % ), oběžnou dobu (Orbital period – dny) a plošnou rychlost (Swept area during a time step – AU ² /den ).

Plugin, jak vidíte, nabízí celkem netradiční možnosti vykreslování a výpočtů pohybů oběžnic kolem Slunce a jako takový velmi dobře poslouží například v rámci astronomických kurzů.

Za výpomoc se zpracováním článku děkuji kolegům z Kosmologické sekce České astronomické společnosti a jejímu předsedovi ing. Vladimíru Novotnému.

Návod byl vytvořen v OpenOffice.org 3.3.